One variable Frequently the term linear equation refers implicitly to the case of just one variable In this case, the equation can be put in the form =, and it has a unique solution = − in the general case where a ≠ 0In this case, the name unknown is sensibly given to the variable x If a = 0, there are two casesEither b equals also 0, and every number is a solutionFirst of all it offers two methods to solve the slope line equation as detailed here 1 st approach is the one that requires both coordinates of the two points to be given;How many Americans start with S ?

5 4 Writing Equations In Point Slope Form Ppt Download
Y^2-y^1/x^2-x^1 formula
Y^2-y^1/x^2-x^1 formula-Simple and best practice solution for m=(y_1y_2)/(x_1x_2) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkGradient of a line (EMA6B) Gradient The gradient of a line is determined by the ratio of vertical change to horizontal change Gradient (\(m\)) describes the



Graphing Parabolas
Apr 05, · The formula for finding the slope of a line on a coordinate plane is (y2 y1) / (x2 x1), where (x2, y2) and (x1, y1) represent two distinct points on the line This is also known as "change in y over change in x" or "rise over run"Formula Sheet Below are the formulas you may find useful as you work the problems However, some of the formulas may not be used You may refer to this page as you take the test As sessment Syst em Georgia Milestones Linear Formulas Slope Formula m = y 2 – y 1}x 2 – x 1 Linear Equations Slopeintercept Form y = mx b Pointslope Form yThe x and y coordinates of the lines are used to calculate the slope of the lines It is the ratio of the change in the yaxis to the change in the xaxis The formula to calculate slope is given as, Slope of a Line m = y2 y1 / x2 x1 Where m is the slope of the line x1, x2 are the coordinates of xaxis and y1, y2 are the coordinates of yaxis
This preview shows page 17 19 out of 70 pages Solve Find the slope m = y 2y 1 _ x 2x 1 Slope formula = 937 997 _ 8 4 Let (x 1, y 1) = (4, 997) and (x 2, y 2) = (8, 937) = 06 _ 4 or 015 Simplify Use (8, 937) to find the yintercept of the line y = m x b Slopeintercept form 937 = 015 (8) b Replace y with 937, m with 015, and x with 8 937 = 12 b SimplifyMar 11, 18 · `m=(y_2y_1)/(x_2x_1` Interactive graph slope of a line You can explore the concept of slope of a line in the following interactive graph (it's not a fixed image) Drag either point A (x 1, y 1) or point B (x 2, y 2) to investigate how the gradient formula works The numbers will update as you interact with the graphEnter any Number into this free calculator $ \text{Slope } = \frac{ y_2 y_1 } { x_2 x_1 } $ How it works Just type numbers into the boxes below and the calculator will automatically find the slope of two points How to enter numbers Enter any integer, decimal or fractionFractions should be entered with a forward slash such as '3/4' for the fraction $$ \frac{3}{4} $$
Feb 18, 09 · there is not any real thank you to simplify that, yet you may desire to FOIL it As a refresher FOIL = FIRST (of each and each element), exterior (of each and each element), indoors (of each and each element) and extremely final (of each and each element) (xa million)(x2) FIRST multiply x by making use of making use of x exterior multiply x by making use of makingThe slope m of the line through any two points (x 1, y 1) and (x 2, y 2) is given by The yintercept b of the line is the value of y at the point where the line crosses the y axis Since for point (x 1, y 1) we have y 1 = mx 1 b, the yintercept b can be calculated bySlope formula and its process The formula for determining slope is not hard in any manner Consider that you have (X1, Y1), (X2, Y2) as the pairs of values being used If these points are being considered, the formula of the scope would be given as follows Slope = Y2Y1/X2X1



3 Ways To Solve Systems Of Algebraic Equations Containing Two Variables



Solved 1 Quadratic Equations A Solve The Quadratic Equ Chegg Com
2 nd method is the one that takes account of at least the coordinates of one point plus either the slope or the angle in incline;Substituting both quantities into the above equation generates the formula m = y 2 − y 1 x 2 − x 1 {\displaystyle m={\frac {y_{2}y_{1}}{x_{2}x_{1}}}} The formula fails for a vertical line, parallel to the y axis (see Division by zero ), where the slope can be taken as infinite , so the slope of a vertical line is considered undefinedThen, as per the slope formula, If Slope of XY = Slope of YZ = Slope of XZ, then the points X, Y and Z are collinear Note Slope of the line segment joining two points say (x 1, y 1) and (x 2, y 2) is given by the formula m = (y 2 – y 1)/ (x 2 – x 1) Example Show that the three points P(2, 4), Q(4, 6) and R(6, 8) are collinear
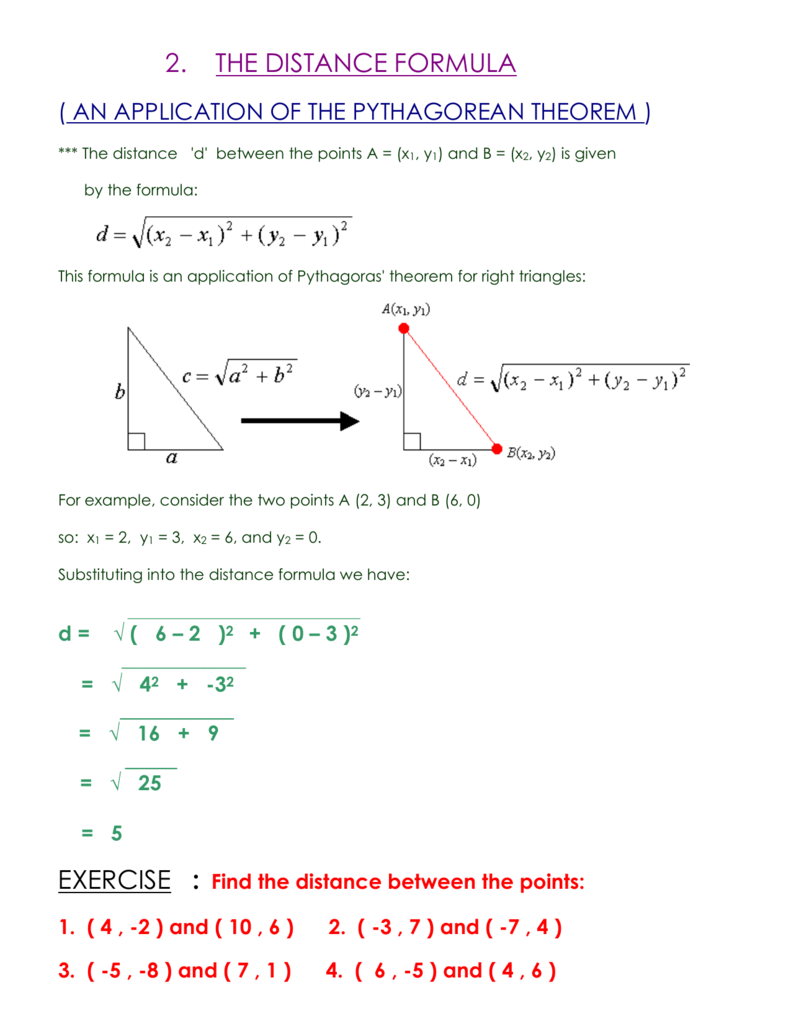


The Distance D Between The Points A X1 Y1 And B X2 Y2



Graphing Parabolas
Apply the following formula Slope = y 2y 1 x 2x 1 Example Slope = 141 81 = 13 7 = 18 (Close these directions)Let f(x,y)=1/(x^2y^2) for (x,y)\neq 0 Determine whether f is integrable over U0 and over \mathbb{R}^2\bar{U};Formula Sheet Below are the formulas you may find useful as you work the problems However, some of the formulas may not be used You may refer to this page as you take the test Assessment System Georgiargia Mileststonesnes Linear Formulas Slope Formula m = y 2 – y 1}x 2 – x 1 Linear Equations Slopeintercept Form y = mx b Pointslope
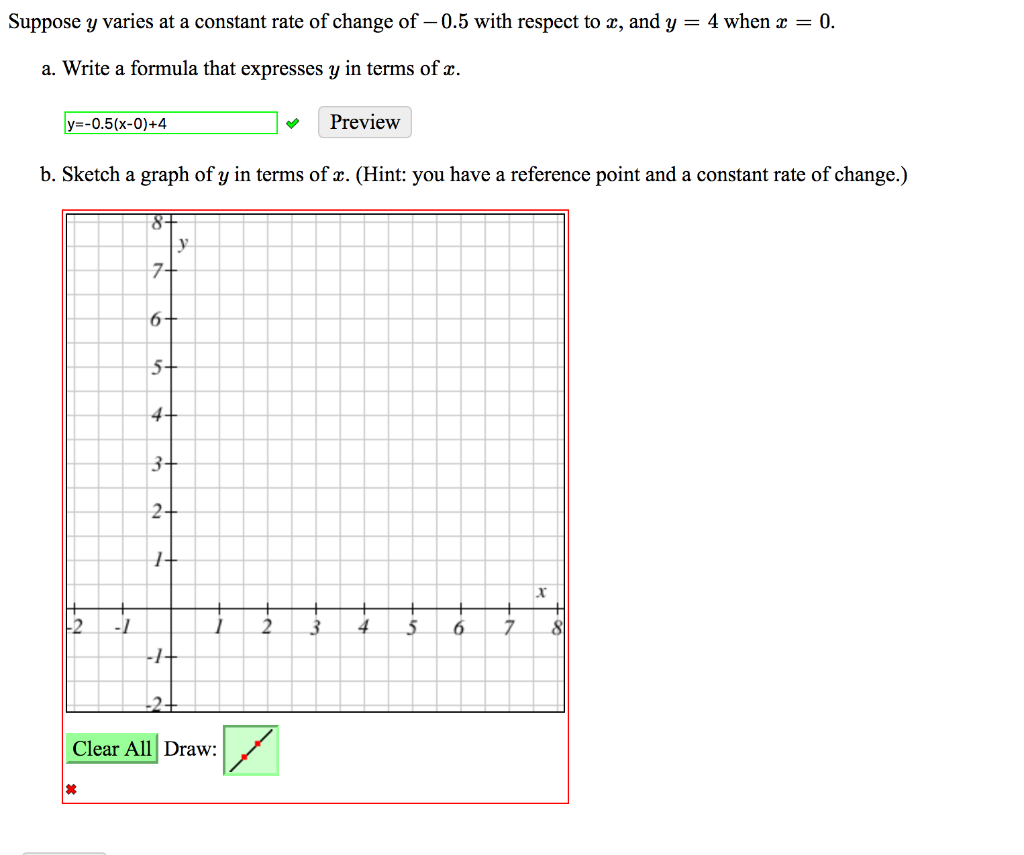


Solved Suppose Y Varies At A Constant Rate Of Change Of 3 Chegg Com



5 4 Writing Equations In Point Slope Form Ppt Download
Y 2 y 1 x 2 x 1 In the equation above, y 2 y 1 = Δy, or vertical change, while x 2 x 1 = Δx, or horizontal change, as shown in the graph provided It can also be seen that Δx and Δy are line segments that form a right triangle with hypotenuse d, with d being the distance between the points (x 1, y 1) and (x 2, y 2)Thanks to all of you who support me on Patreon You da real mvps!What is the formula to calculate slope intercept form?



X1 X2 Y1 Y2 Distance Formula Page 1 Line 17qq Com



Graphing Formulas
Looking at we can see that the equation is in slopeintercept form where the slope is and the yintercept is Since this tells us that the yintercept is Remember the yintercept is the point where the graph intersects with the yaxis So we have one point Now since the slope is comprised of the "rise" over the "run" this meansSep 26, 19 · See how to find the slope of a line on a graph using the slope formula, rise over run and get shortcuts for parallel and perpendicular line slopes M = (Y 2 – Y 1) / (X 2 – X 1) The answer, M, is the slope of the line It can be a positive or negative valueFormula Sheet Below are the formulas you may find useful as you work the problems However, some of the formulas may not be used You may refer to this page as you take the test As sessment Syst em Georgia Milestones Linear Formulas Slope Formula m = y 2 – y 1}x 2 – x 1 Linear Equations Slopeintercept Form y = mx b Pointslope Form y
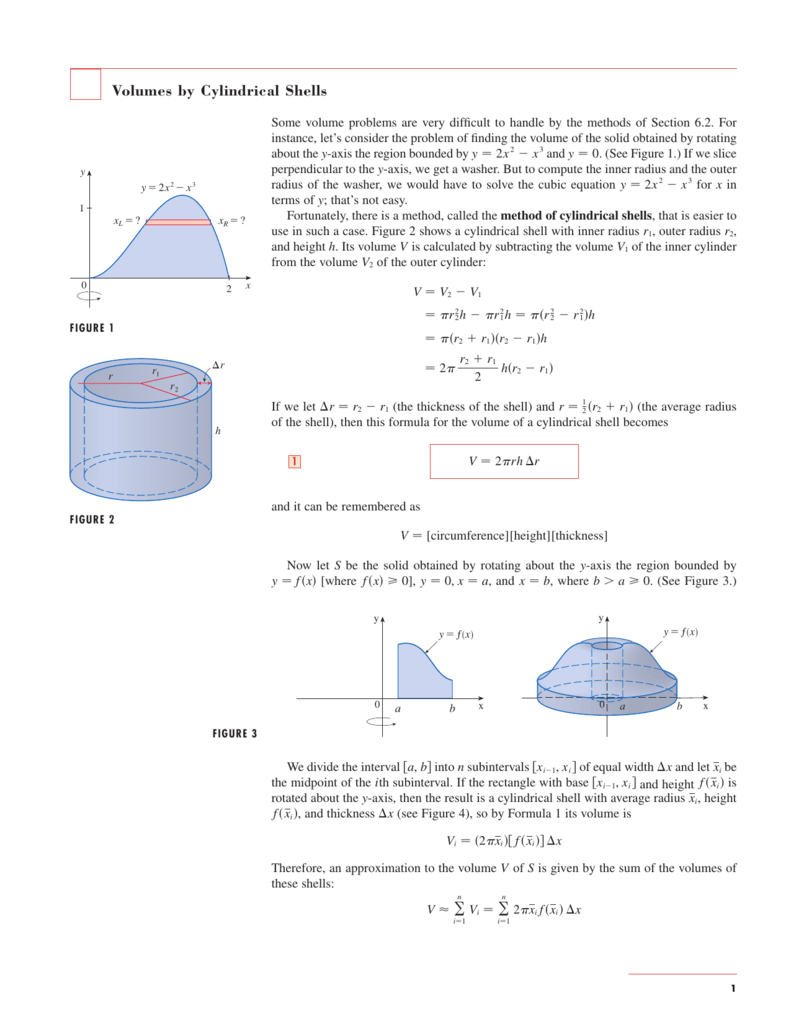


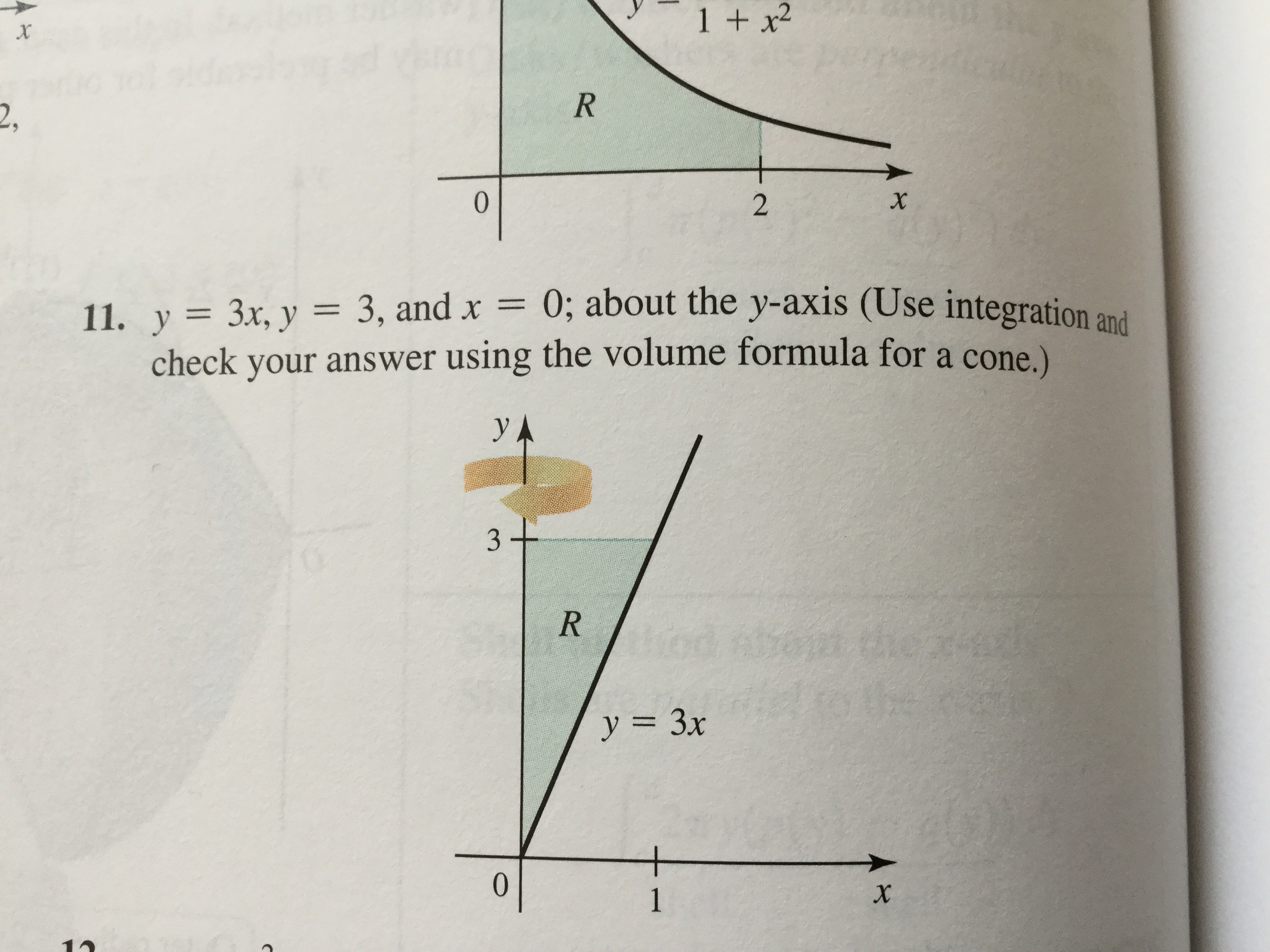
Volumes By Cylindrical Shells


Multiplicative Inverse Wikipedia
Find the measure of the angle θ between u = and v = ?Tangent Circle Formula In geometry, a tangent of a circle is a straight line that touches the circle at exactly one point, never entering the circle's interior It is a line through a pair of infinitely close points on the circleCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Worked Example Average Rate Of Change From Equation Video Khan Academy



Solving Rational Equations
Learn how to use the slope formula, m = (y2y1)/(x2x1) to find the slope of a line through two pointsThe algorithm of this slope calculator is based on7 answers Answer questions Answer questions How many of them Amerikana exist ?
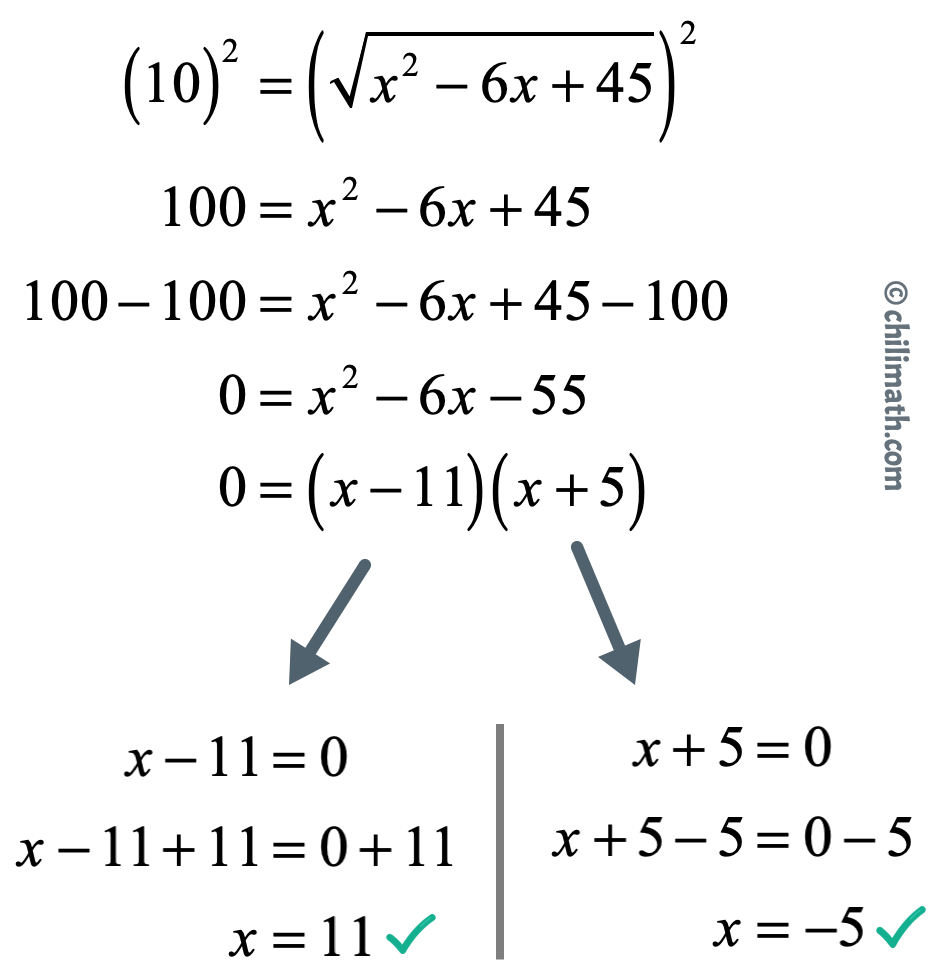


Distance Formula Chilimath



Solved 1 Solve The Following Ordinary Differential Equat Chegg Com
The formula y y1 = m (x x1) is usually described as the 'pointslope form' for the equation of a line It is useful because if you know one point on a certain line and the slope of that certain line, then you can define the line with this type of formula11 answers how to find the area of a circle 12cm?Simple and best practice solution for y2y1/x2x1 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,



Midpoint Formula How To Find Midpoint Equation Tutors Com



Graphing Parabolas
Calculates the linear equation, distance and slope given two pointsThe slope #m# of a linear equation can be found using the formula #m= (y_2 y_1)/(x_2x_1)#, where the #xvalues# and #yvalues# come from the two ordered pairs #(x_1,y_1)# and #(x_2,y_2)#, What is an equivalent equation solved for #y_2#?Distance formula d = (x 2 Slope equation m = y 2 − y 1 x 2 − x 1 m = \frac{y_2y_1}{x_2 x_1} m = x 2
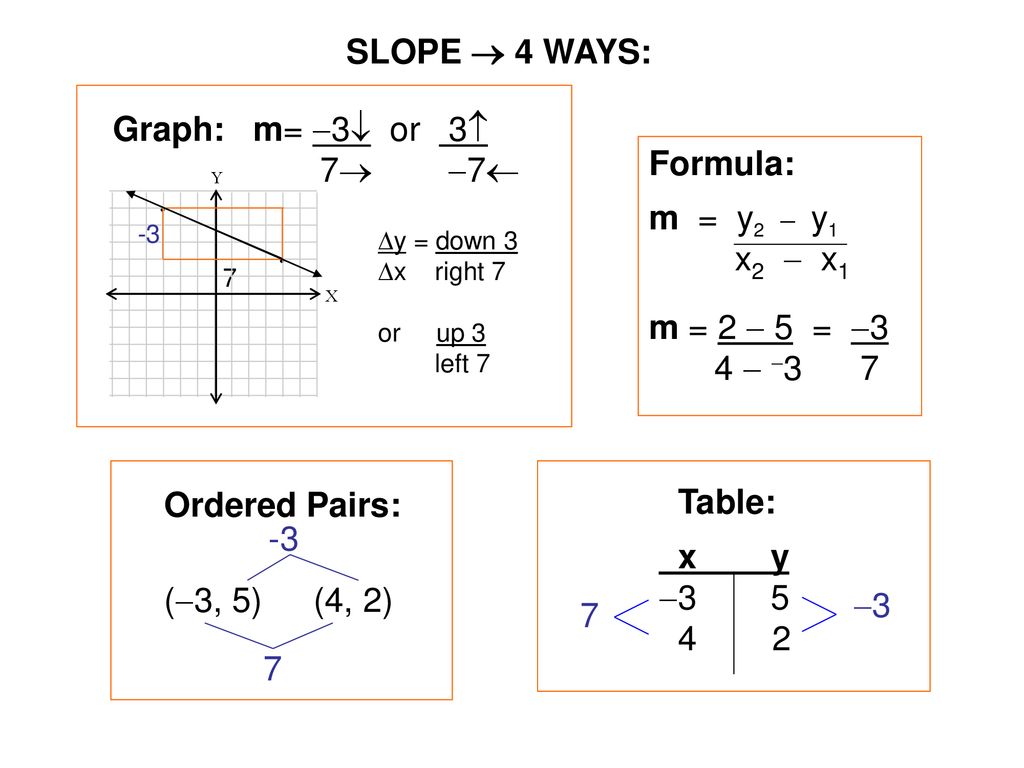


Slope 4 Ways Graph Formula Ordered Pairs Table Ppt Download



Distance Formula Given The Two Points X1 Y1 And X2 Y2 The
$\begingroup$ The standard formula for the distance between $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_1 x_2)^2 (y_2 y_2)^2}$ Since $(x_1 x_2)^2= (x_2 x_1)^2$ and $(y_1 y_2)^2= (y_2 y_1)^2$, no, the order does not matter $\endgroup$ – user May 31 '19 at 1933Two Point form Formula Where, X1 , X2 = X Axis Points Y1, Y2 = Y Axis Points X, Y = Axis Equation of a straight line can be calculated using various methods such as slope intercept form, point slope form and two point slope form Two Point form is one such method used to find the equation of a straight line when there is no slope and theQuadratic Formula To solve ax2 bx c= 0, a6= 0, use x= 2b p b 4ac 2a The Discriminant The discriminant is the part of the quadratic equation under the radical, b2 4ac We use the discriminant to determine the number of real solutions of ax2 bx c= 0 as such 1 If b2 4ac>0, there are two real solutions 2 If b2 4ac= 0, there is one
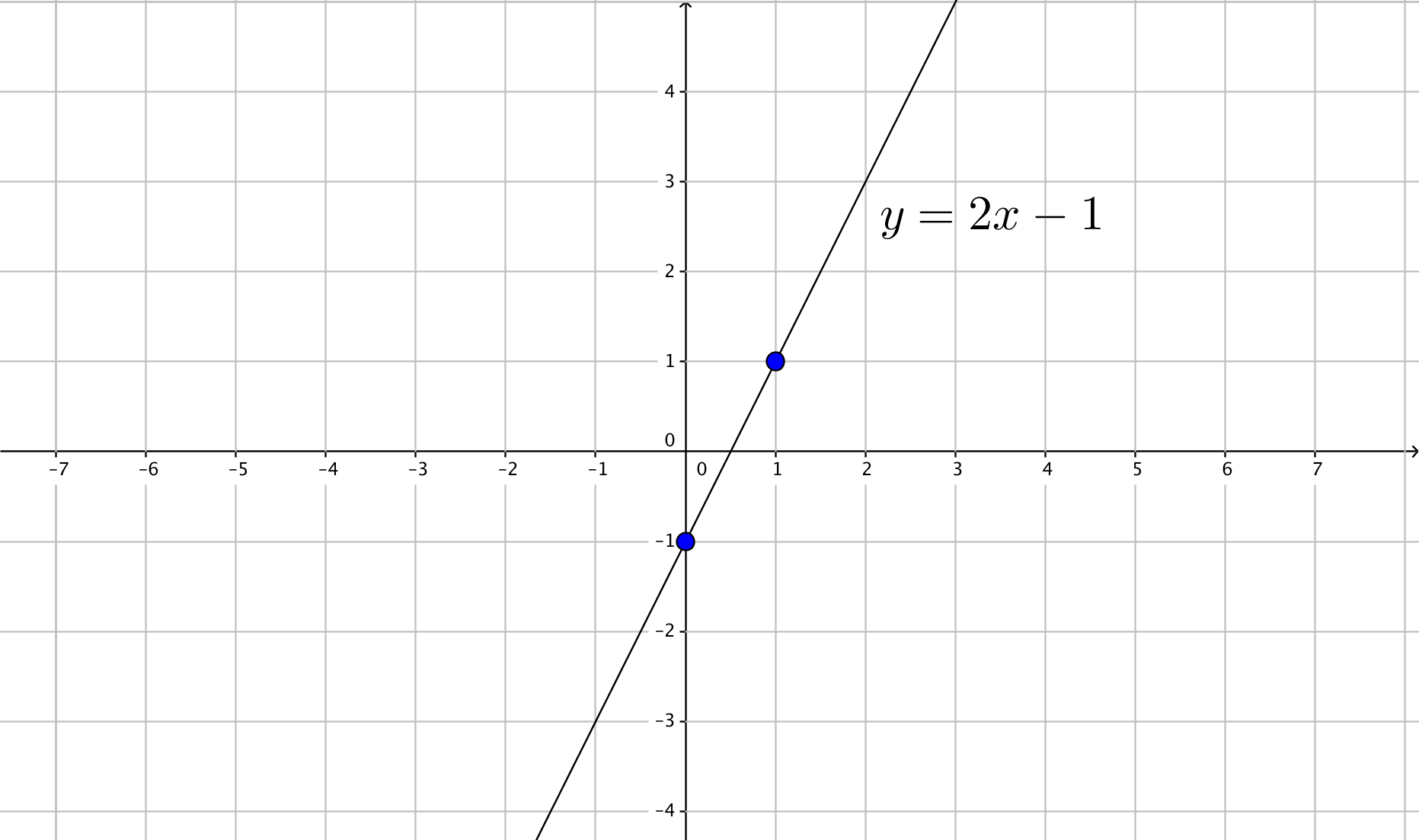


How Do You Graph Y 2x 1 By Plotting Points Socratic
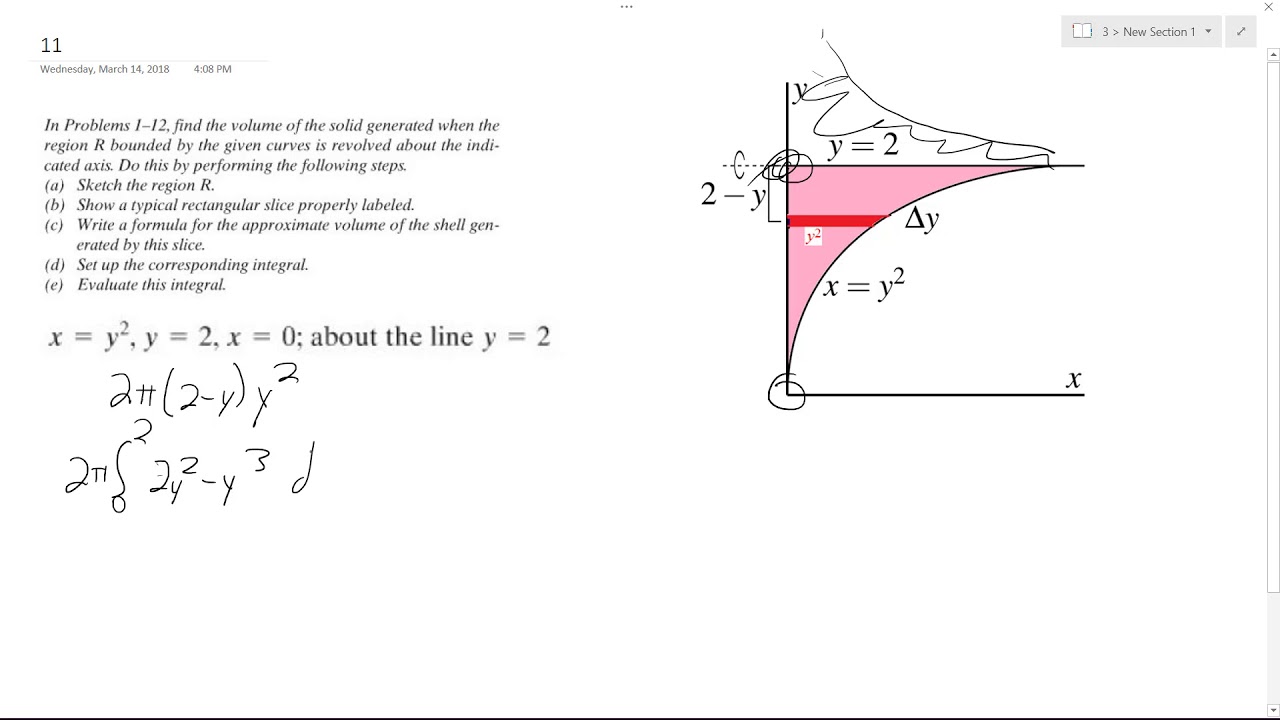


X Y 2 Y 2 X 0 About The Line Y 2 Youtube
$1 per month helps!!Formula k = (y 2y 1) / (x 2x 1) Where, k = Gardient of Line x1, x2, y1, y2 = Point of Coordinates Related Calculator Gradient of Line in a Plane Calculator;Formula Look at the Framework and see how this relates to the algebra and function standards for your grade PRIMARY CONTENT MODULE Algebra Linear Equations & Inequalities T 56 y 2 – y1 x 2 – x1 = 5 – (–2) 6 – 1 = 7 5 Step 2 y = 7 5 x b Substitute x = 1 and y = –2 into the equation above –2 = 7 5 (1) b



Linear Equations And Systems Slope Equation Forms Of Lines


Linear Functions And Slopes Ppt Download
Step 1 Calculate the slope (y 2 y 1) / (x 2 x 1) Step 2 Calculate where the line intersects with the yaxis by entering one of the coordinates into this equation y mx = b Example To calculate the slopeintercept equation for a line that includes the two points ( 7, 4) and (1, 1) Step 1 slope (m) = (1 4) / (1 7) = 3 / 6 slopeY 2 y 1 x 2 x 1 = rise run Lines can be represented in three di erent ways Standard Form ax by = c SlopeIntercept Form y = mx b PointSlope Form y y 1 = m(x x 1) where a;b;c are real numbers, m is the slope, b (di erent from the standard form b) is the yintercept, and (x 1;y 1) is any xed point on the line 5 Circles A circle, sometimes denoted JLet's use the example of the line \(x = 4\), which is graphed above Two points on this line would be \((4, 1)\) and \((4, 2)\)



How To Find The Distance Between Two Points 6 Steps
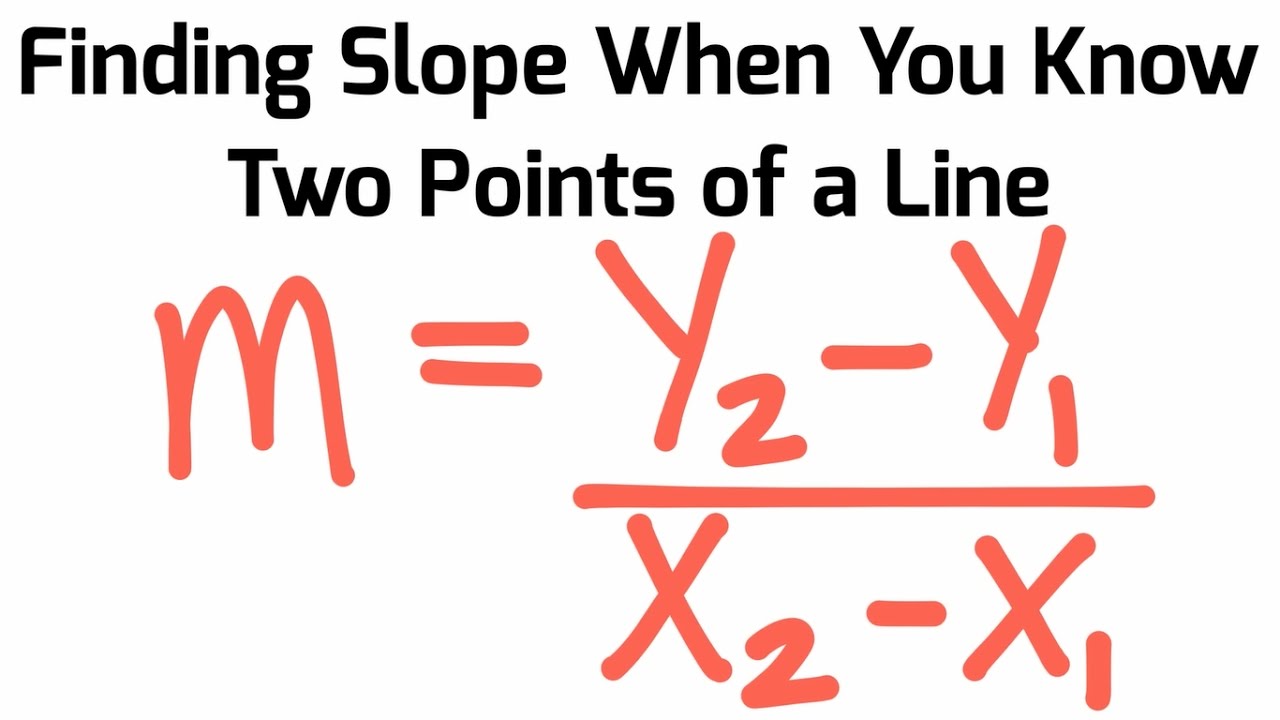


Equation For Slope Of Two Points Youtube
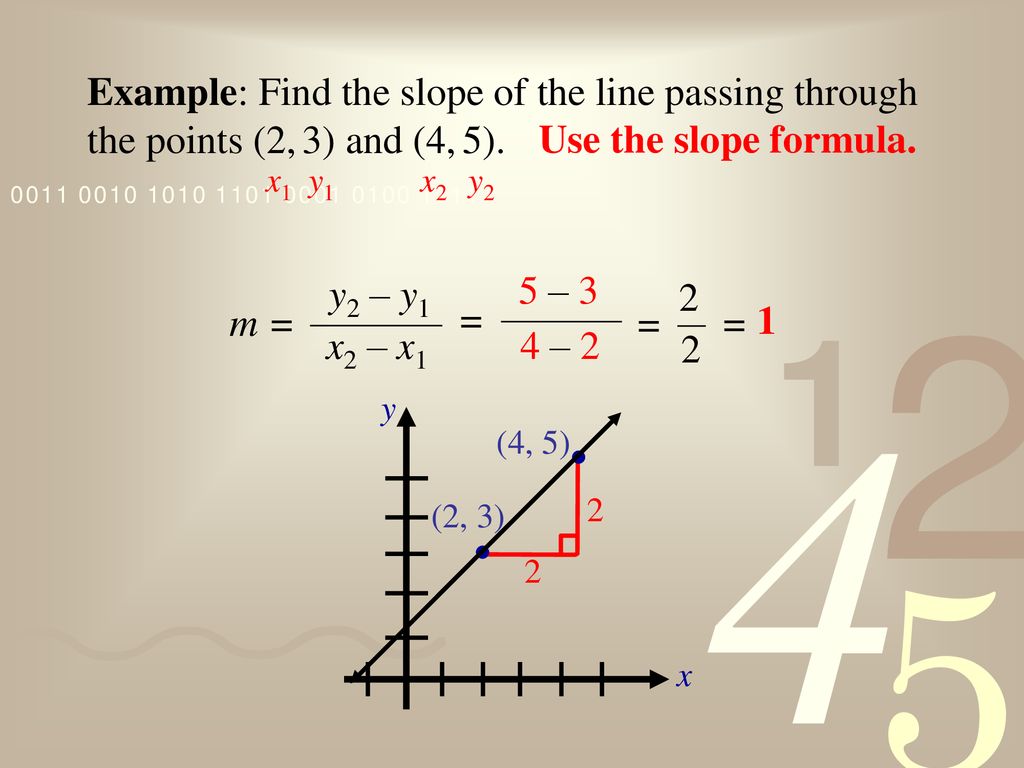
11 answers solve for x?\((m)\) = \(\frac {y_2 – y_1}{x_2 – x_1} = \frac {7 – 1} {4 – 2} = \frac {6}{2} = 3\) Step # 3 Get check the result and you ought to make sure that this slope make sense by thinking about the points on the coordinate plane Also, you can try this formula (m=y2y1/x2x1 calculator) to find the slope of the line or given coordinatesTo understand the discussion below, you should be familiar with finding the slope using the slope formula Why is the slope undefined for vertical lines?
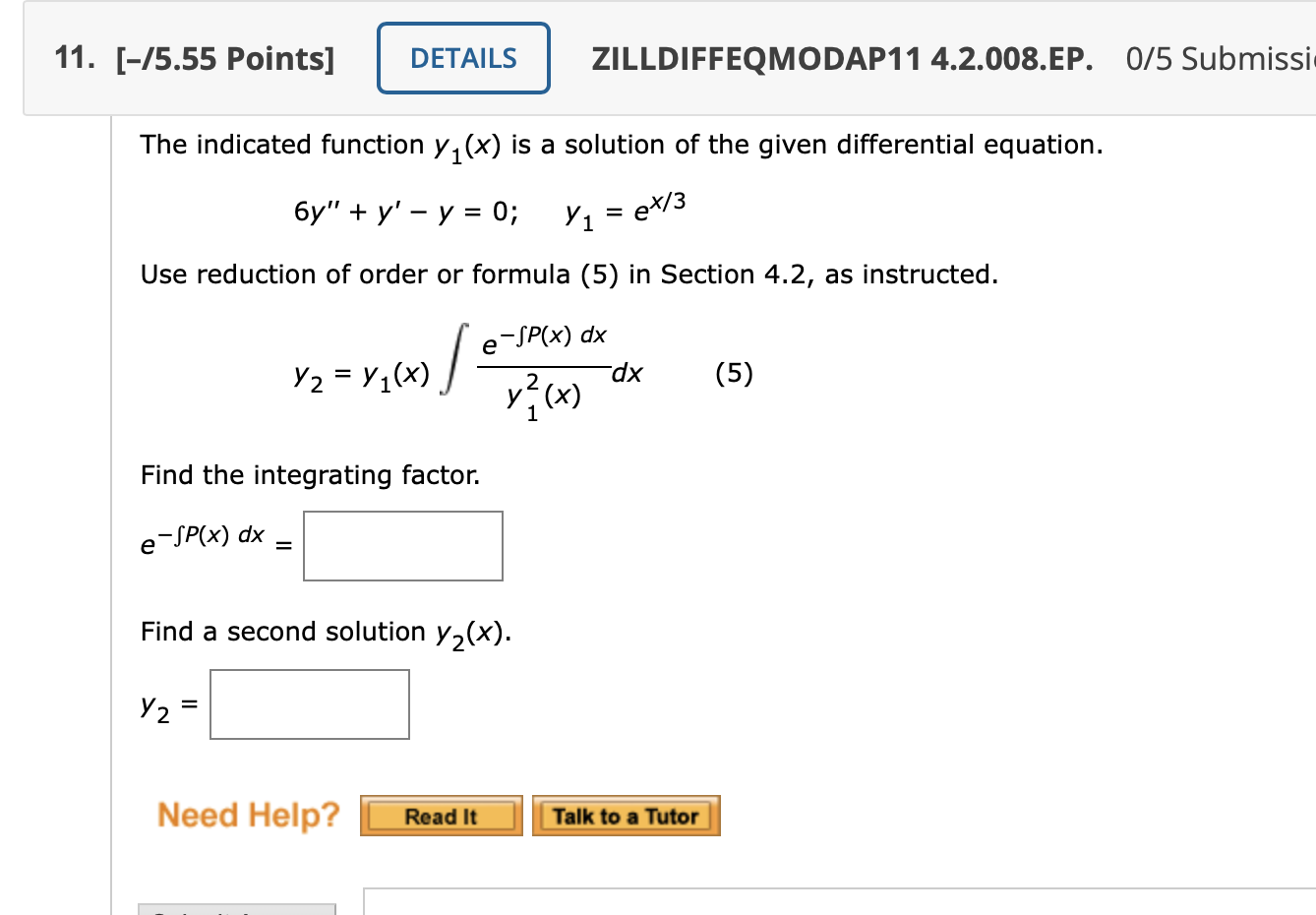


Solved The Indicated Function Y1 X Is A Solution Of The Chegg Com



X1 X2 Y1 Y2 Distance Formula Page 1 Line 17qq Com
First, slope is change in y over change in x, or rise over run Plugging these points in, (y2y1)/ (x2x1)= (68)/ (43), or 14/7, simplifying, the slope= 2 Now, we have y=2xb Using the point (3,8), 8=2*3b, or 8=6b, subtracting 6, 2=b Using slope intercept form, y=mxb, or y=2x2SOLUTION Given m = (y2 y1)/x2 x1), y = mx b, and the points (2, 2) and (2, 4) Find the yintercept Write the equation of the line in slopeintercept form SOLUTION Given m = (y2 y1)/x2 x1), y = mx b, and the points (2, 2) and (2, 4) Find the yinterceptArea of a Segment of a Circle Formula S = r 2 / 2 (α π / 180 sin α) Where, s = Area of a Circle Segment α = Central Angle in Degree
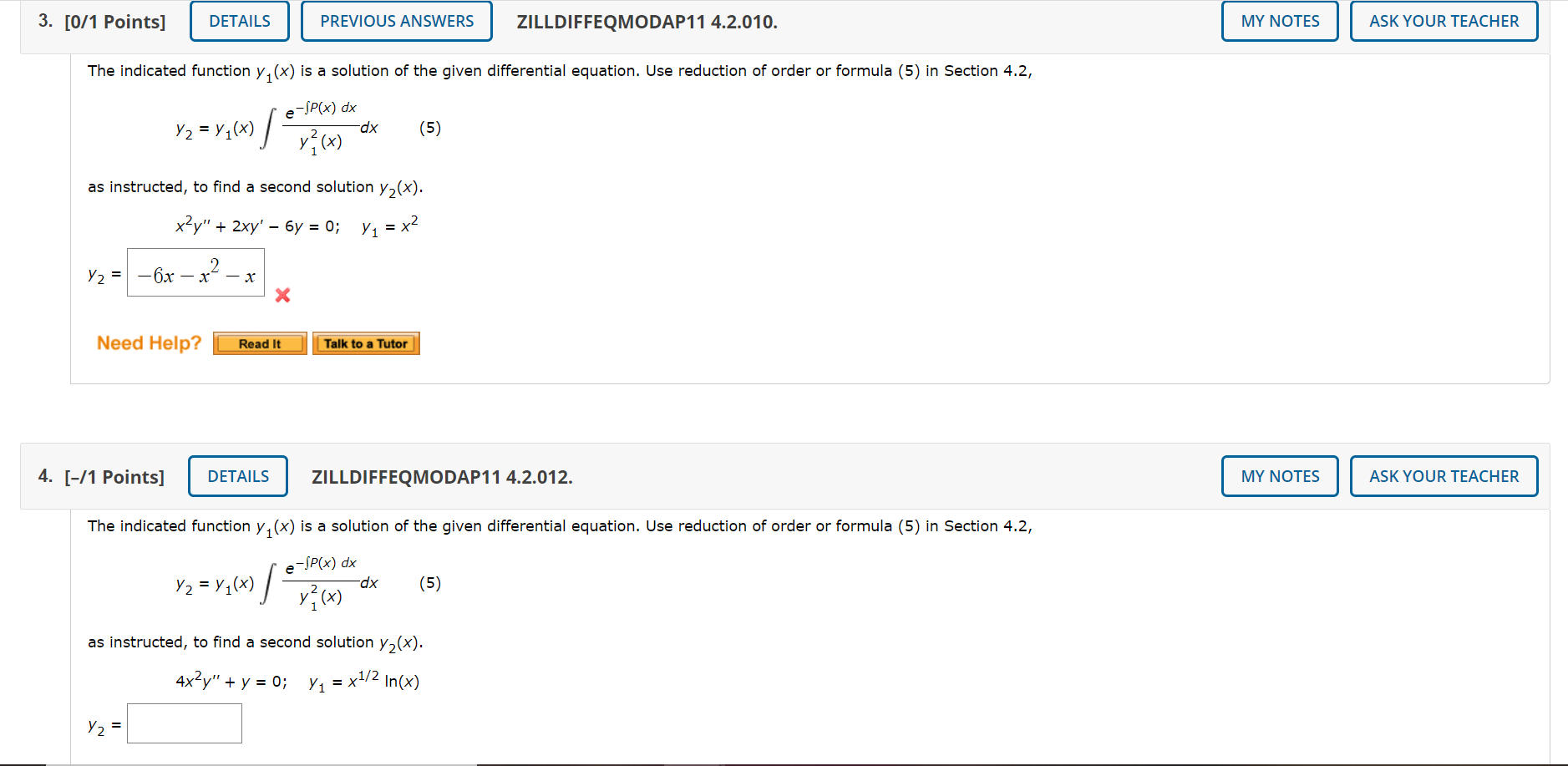


Solved 3 0 1 Points Details Previous Answers Zilldiffe Chegg Com



Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic
Then the first formula converts to the second one as follows m = ( y 1 – y 2 )/( x 1 – x 2 ) = –( y 2 – y 1 )/–( x 2 – x 1 ) = ( y 2 – y 1 )/( x 2 – x 1 ) As you can see above, doing the subtraction in the socalled "wrong" order serves only to create two "minus" signs which then cancel outHow does this slope calculator work?All equations of the form ax^{2}bxc=0 can be solved using the quadratic formula \frac{b±\sqrt{b^{2}4ac}}{2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x=\frac{1±\sqrt{1^{2}4yy}}{2y} This equation is in standard form ax^{2}bxc=0 Substitute y for a, 1 for b, and y for c in the



Finding Inverse Functions Quadratic Example 2 Video Khan Academy



Slope From Equation Video Khan Academy
Simplify (x^2y^2)/ (x^1y^1) x−2 − y−2 x−1 y−1 x 2 y 2 x 1 y 1 Simplify the numerator Tap for more steps Rewrite x − 2 x 2 as ( x − 1) 2 ( x 1) 2 ( x − 1) 2 − y − 2 x − 1 y − 1 ( x 1) 2 y 2 x 1 y 1 Rewrite y − 2 y 2 as ( y − 1) 2 ( y 1) 2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyIf we have the y and x values (as in the coordinates), and c is constant for both points (which if it is two point on one line, we know it is) than we can solve for m with algebra If we have two coordinates on a line (x1,y1 =1,2) and (x2, y2 =3,6) we can solve for m as follows (x2,y2) 6=m3c (x1,y1) 2=m1c
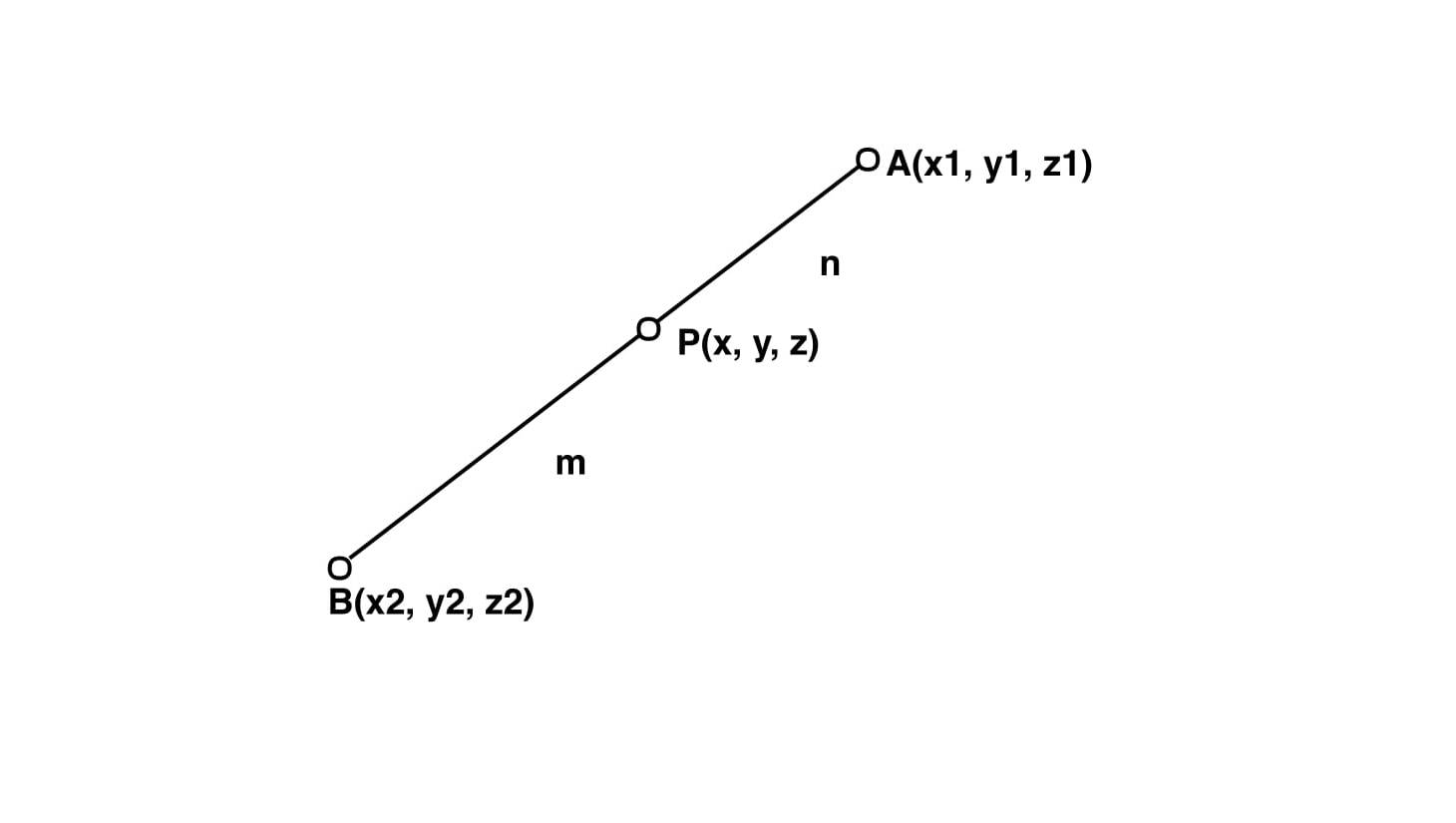


Section Formula For 3 D Geeksforgeeks
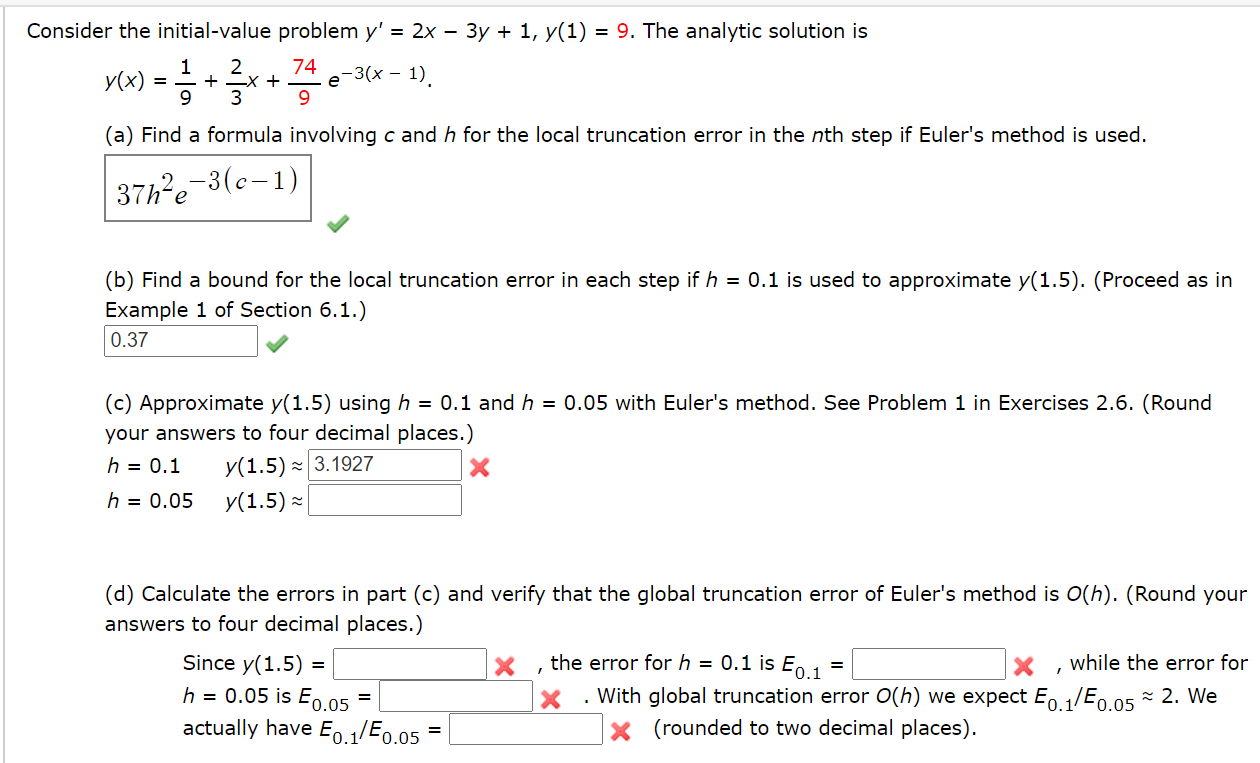


Solved Consider The Initial Value Problem Y 2x 3y Chegg Com
You can put this solution on YOUR website!Find the Equation of a LinJan 19, 15 · Find A using the formula A = Pe^rt?



Ppt Algebra1 The Slope Formula Powerpoint Presentation Free Download Id
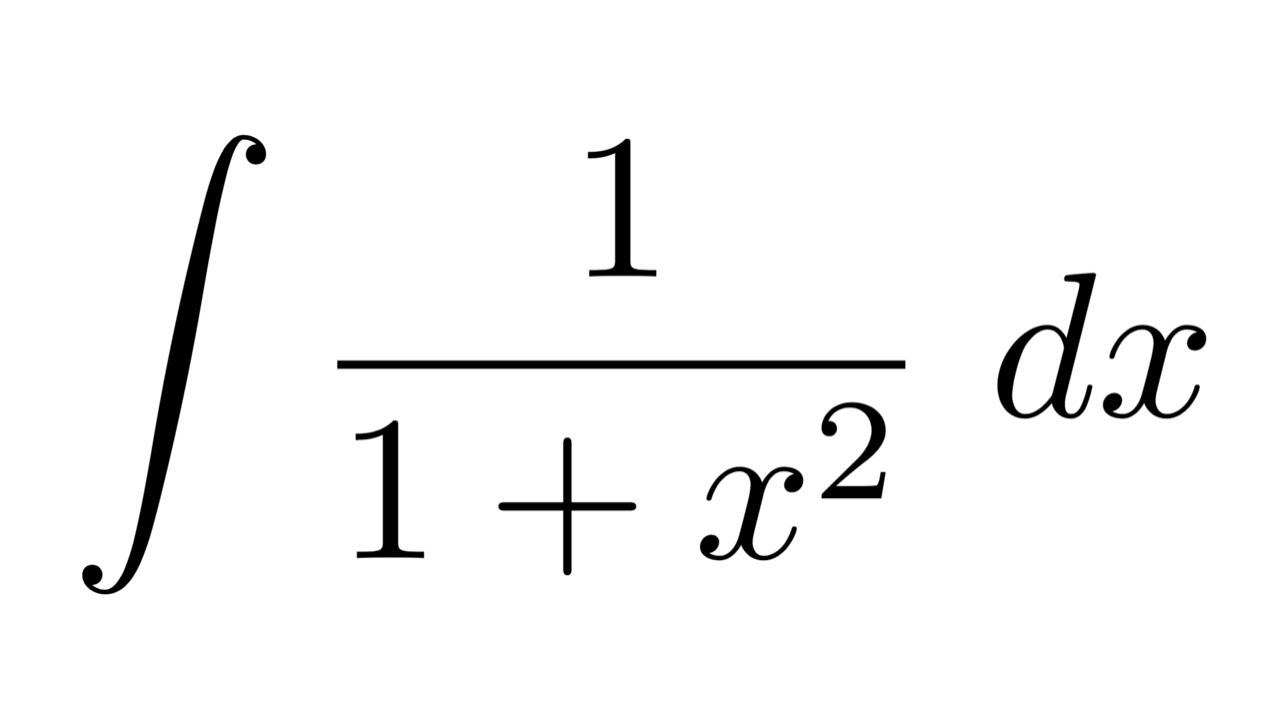


Integral Of 1 1 X 2 Substitution Youtube



Find The Area Of Triangle By Using Formula 1 2 X1 Y2 Y3 X2 Y3 Y1 X3 Y1 Y2 Brainly In



Solved 17 Calculate The Integral Over The Given Region B Chegg Com
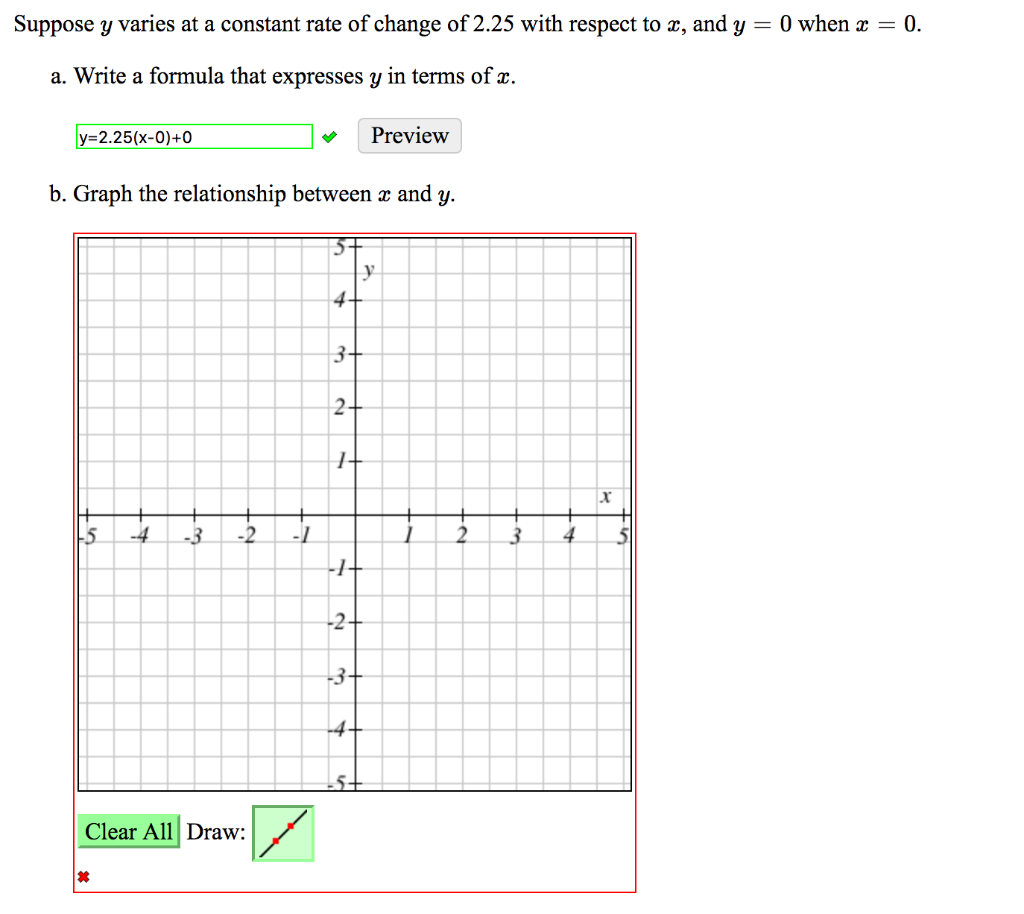


Solved Suppose Y Varies At A Constant Rate Of Change Of 3 Chegg Com



Rate Of Change Ppt Download
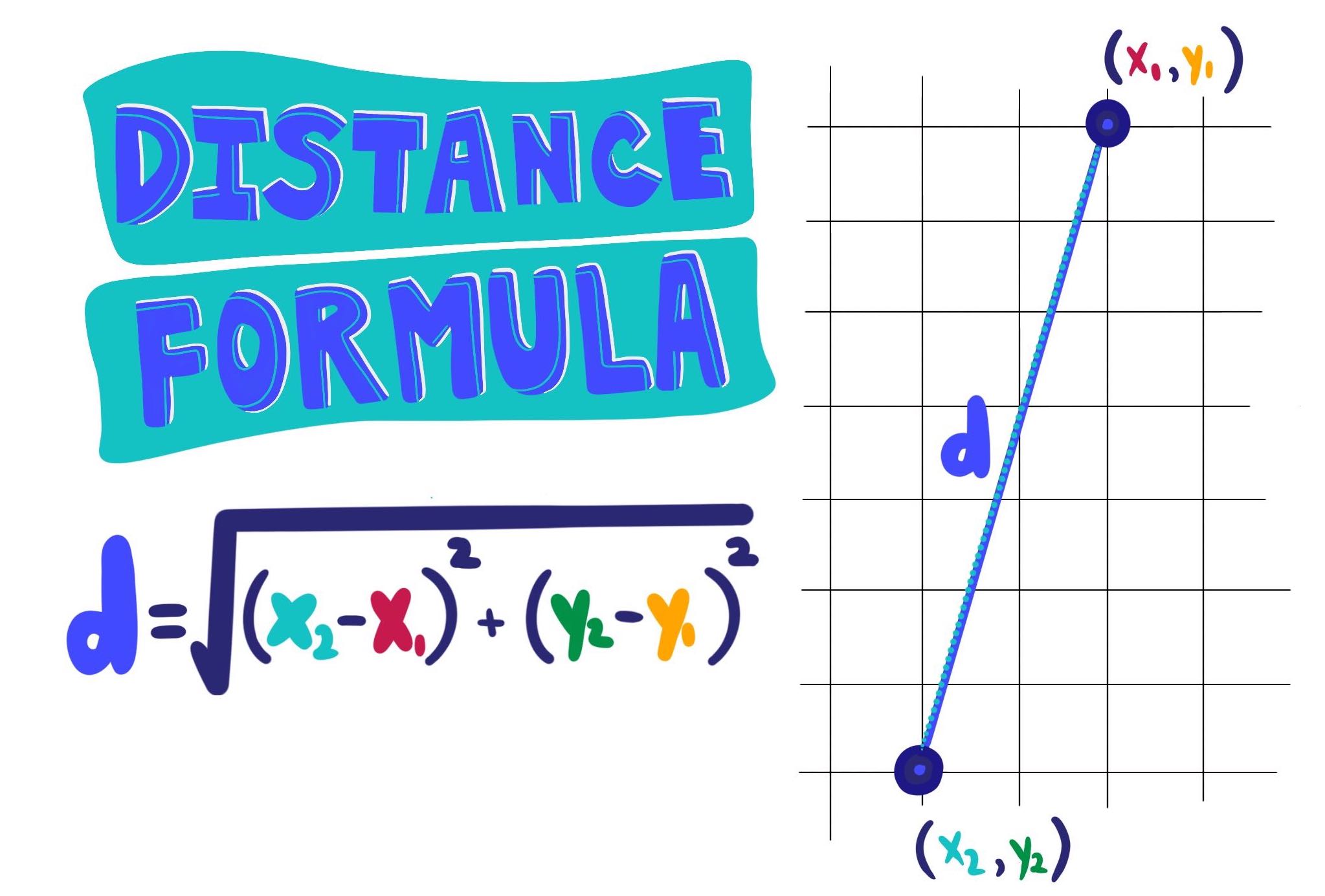


Distance Formula Expii



Mathematics For Machine Learning Linear Regression Least Square Regression By Daksh Deepak K Towards Data Science
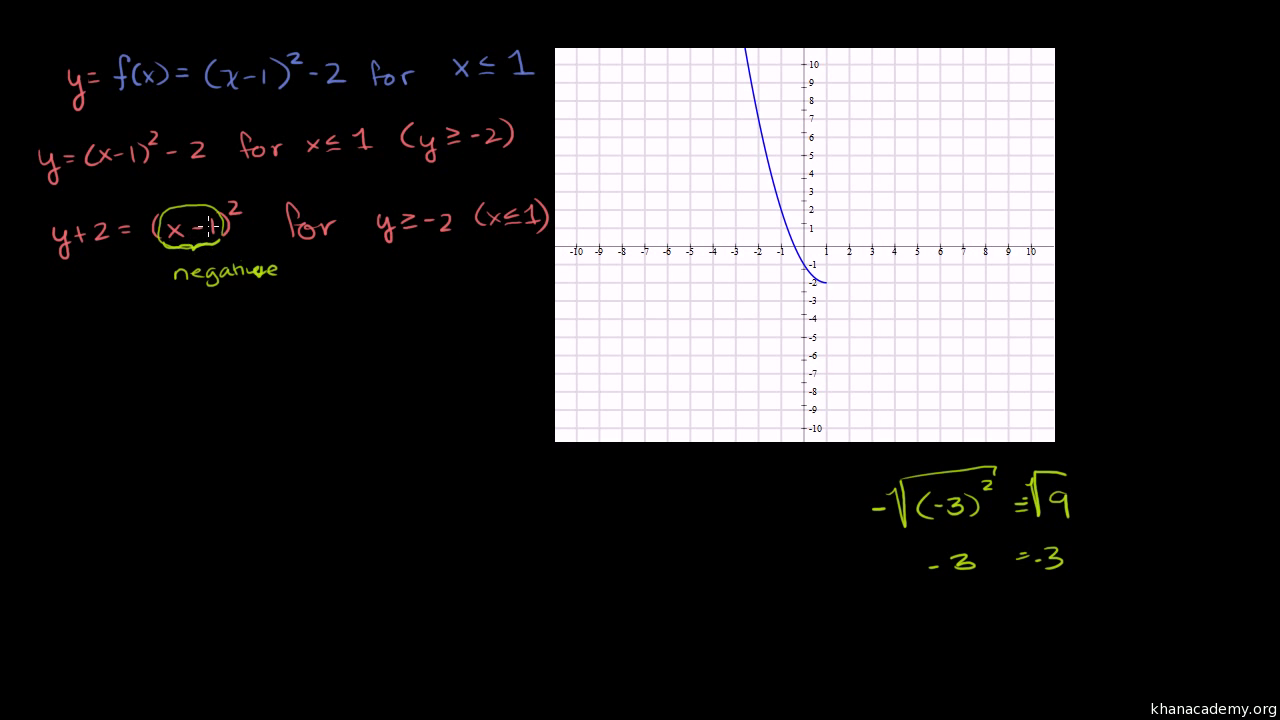


Finding Inverse Functions Quadratic Example 2 Video Khan Academy
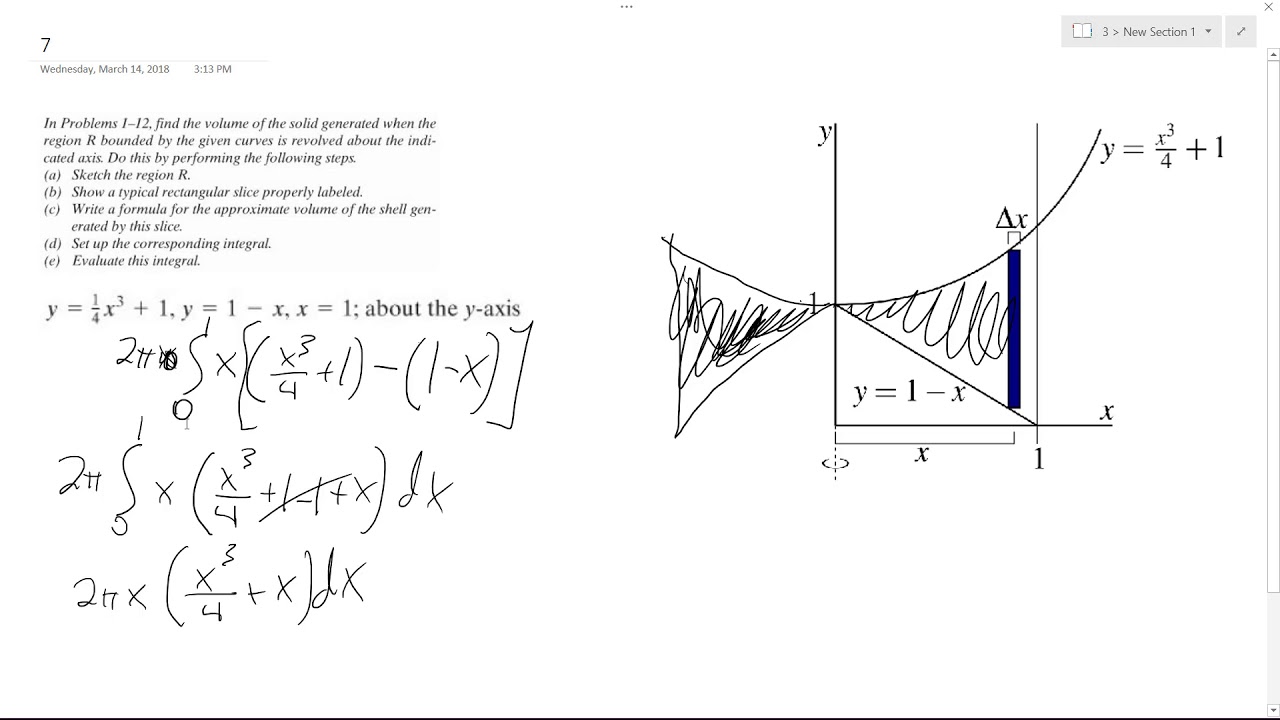


Y 1 4 X 3 1 Y 1 X X 1 About The Y Axis Youtube



2 Partial Differentiation
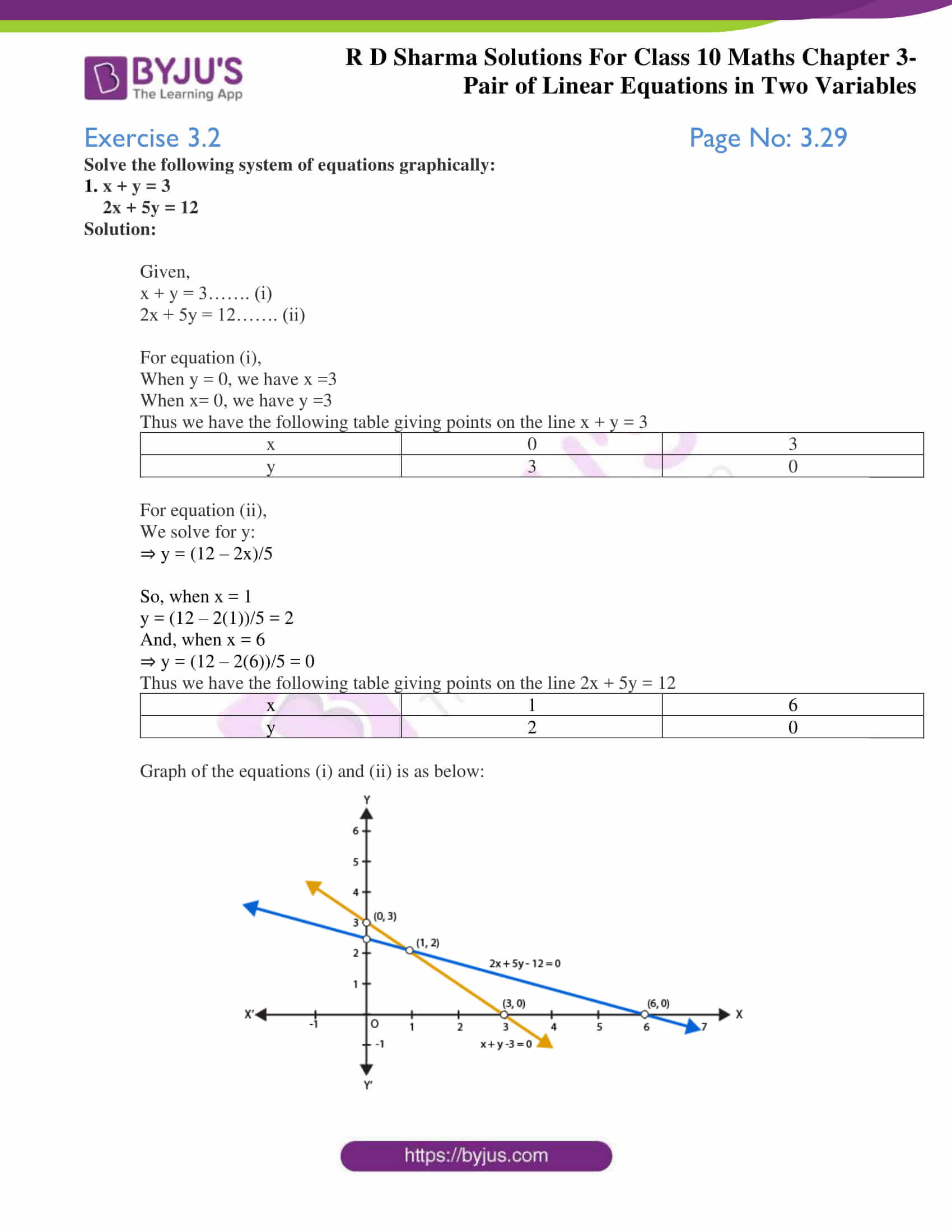


Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



Finding Linear Equations



Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15



Example 27 Solve System Of Equations 2x 5y 1 3x 2y 7



Y1 Y2 X1 X2 Equation Page 1 Line 17qq Com



Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1



Finding A Second Solution To A 2nd Order Differential Equation Mathematics Stack Exchange



Solutions For Review Problems



In The Formula D X2 X1 2 Y2 Y1 2 How Does Each Subtraction Expression Relate To The Brainly Com



Solving Rational Equations



Polynomial Solution Of The Equation 1 X 2 Y 2xy 6y 0 Mathematics Stack Exchange



2 4 And 2 1 Formula Y Y1 Y2 Y1 X2 X1 X X1 Brainly Ph



Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
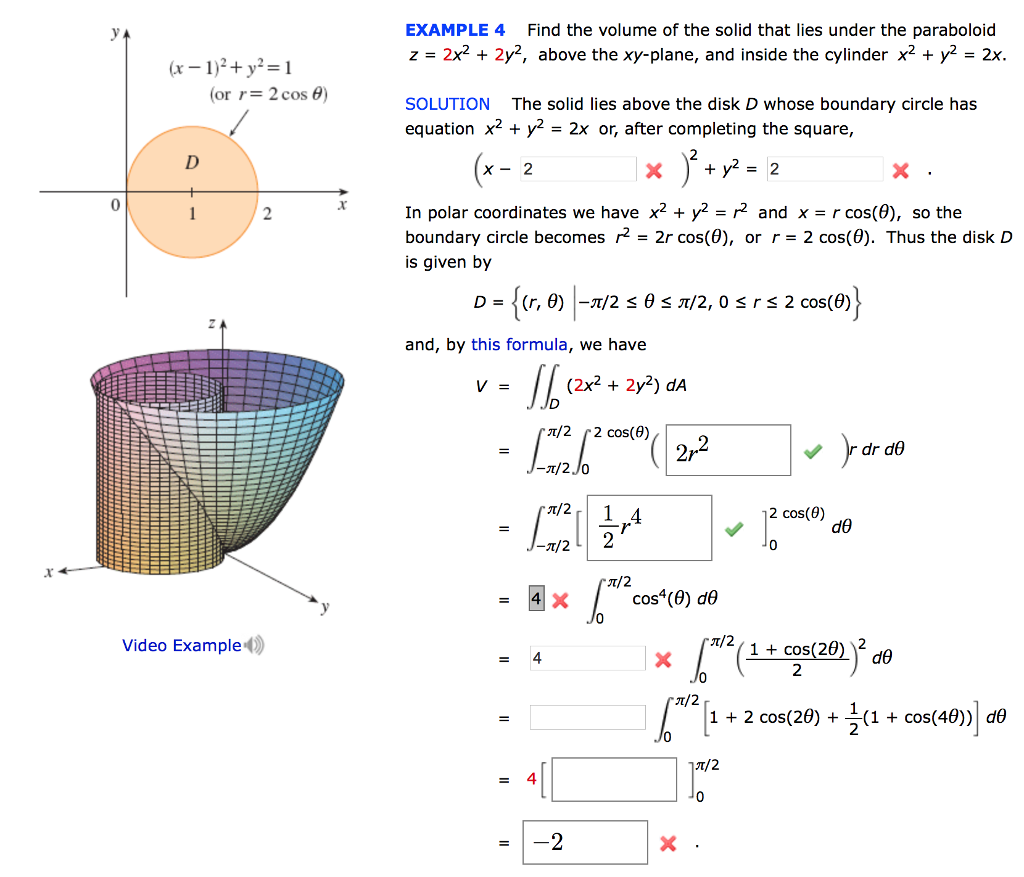


Solved Example 4 Find The Volume Of The Solid That Lies U Chegg Com



Solutions Of Tenth Homework



If A X1 Y1 B X2 Y2 And C X3 Y3 Are Vertices Of Triangle Abc Find Coordinates Of Centroid Youtube



Solve D 2 3d 2 Y E E X Using Method Of Variation Of Parameters Mathematics Stack Exchange



Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1



E Mathematical Constant Wikipedia



Bellwork Use The Slope Formula To Find The Slope Ppt Download
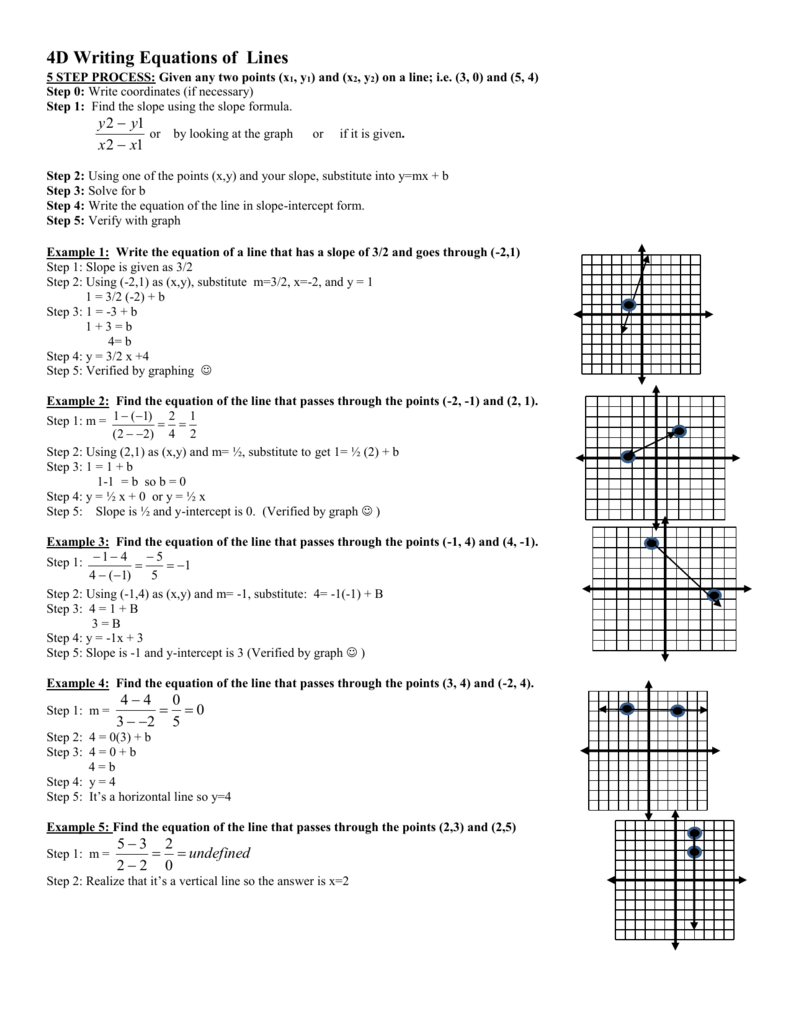


4d Writing Equations Of Lines



13 7 Writing Linear Equations Ppt Download



Graphing X 3 2 Y 3 2 1 Mathematics Stack Exchange



Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy


Solved Example 4 5 And 6 3 Write An Equation For A Circle If The Endpoints Of A Diameter Are At Use The Midpoint Formula To Find The Cente Course Hero



Writing Equations Of Perpendicular Lines Analytic Geometry Video Khan Academy



Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
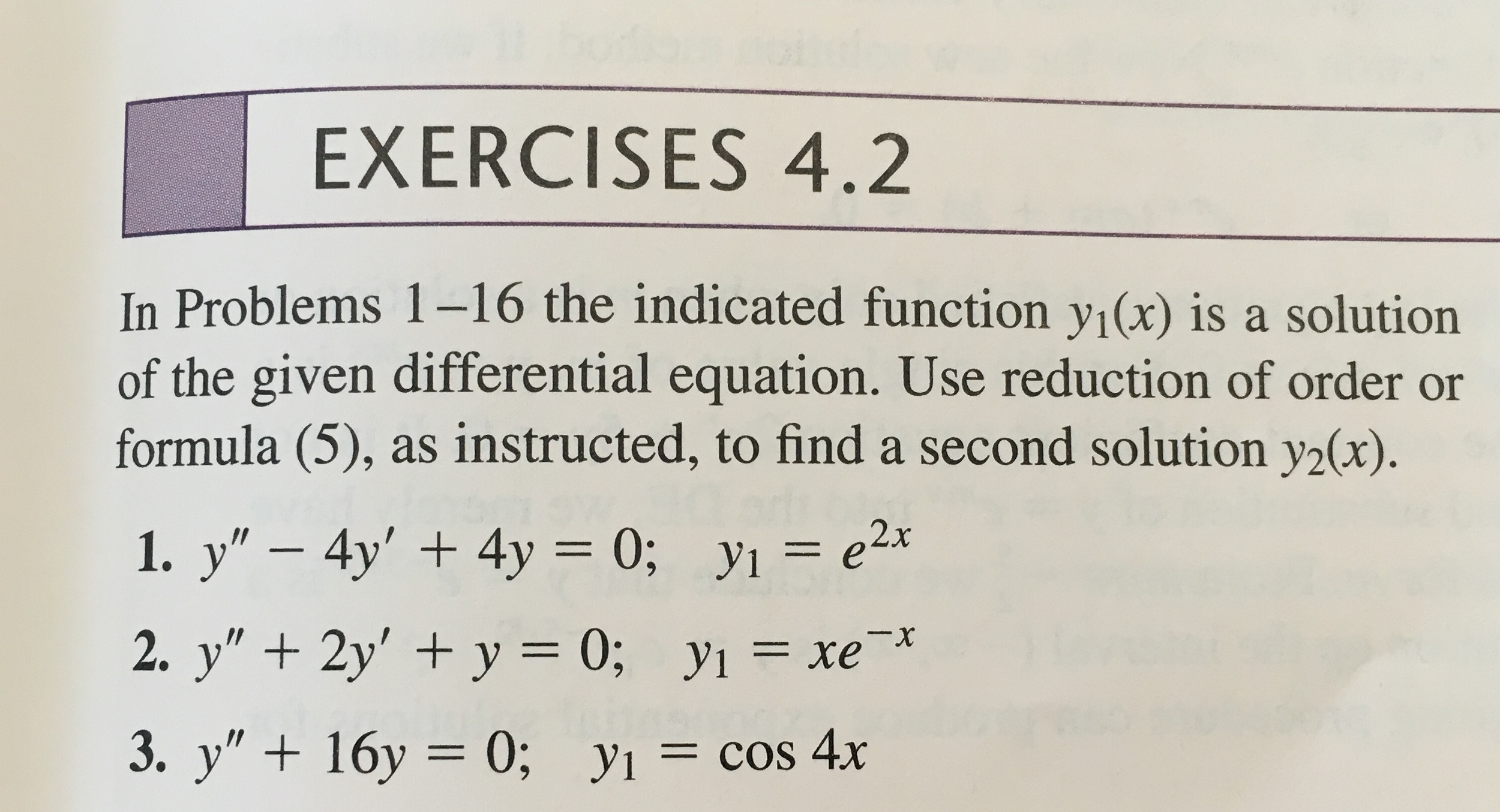


Solved In Problems 1 16 The Indicated Function Y 1 X Is Chegg Com
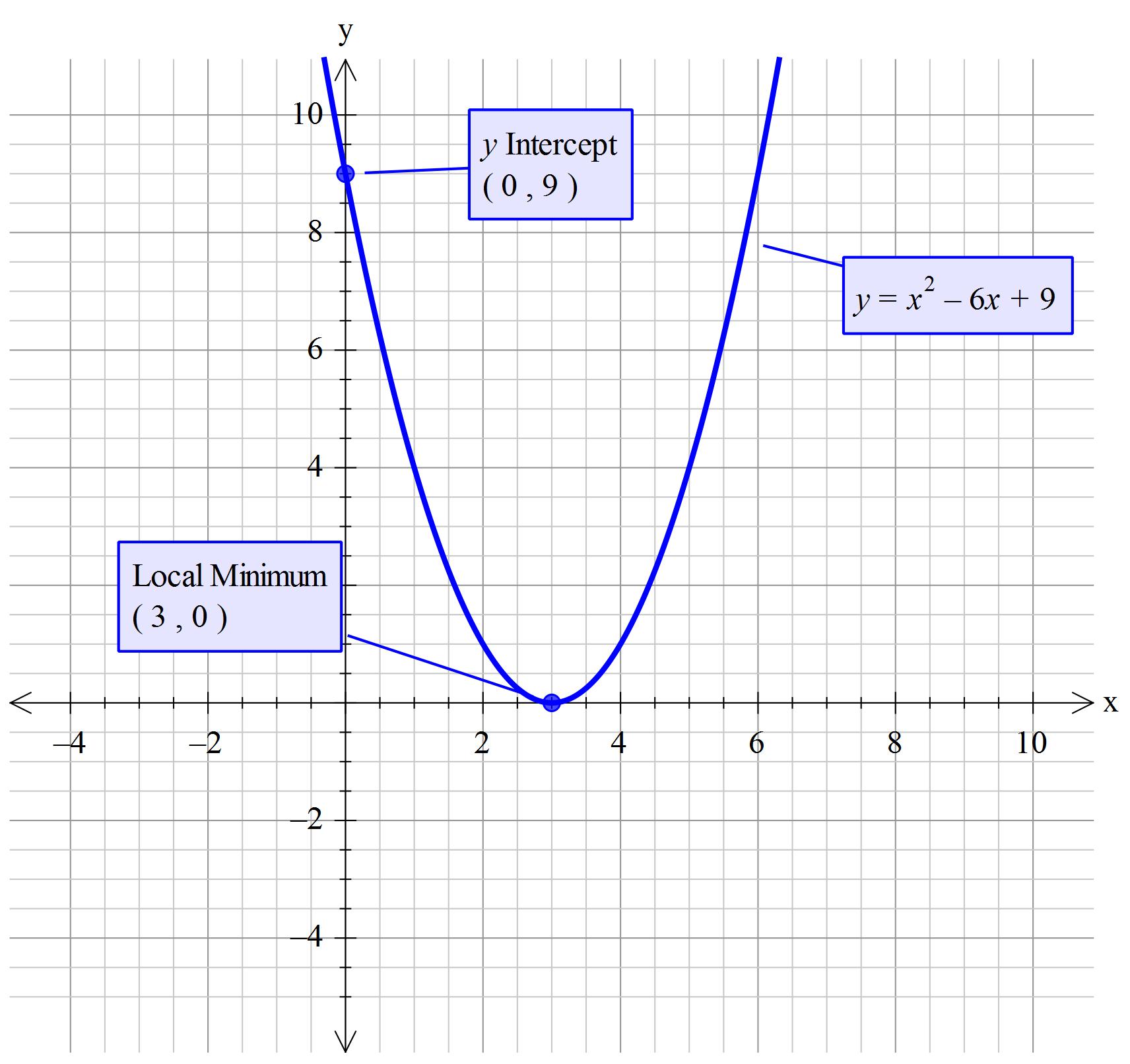


How Do You Solve X 2 6x 9 0 Using The Quadratic Formula Socratic



Answered Problems 9 Given That X X2 And 1 X Bartleby



Graphing Parabolas



Distance Y X C D A B Lengths Parallel To The Axes Are Calculated As If It Was A Number Line Lengths Are Always Positive Examples 1 Calculate The Length Ppt Download



Could Someone Help With Problem 3 Ive Tried X1 X2 But No Matter What I Can T Seem To Get The Answer Askmath



D X2 X1 Y2 Y1 This Is The Formula I Need Number 19 Please Will Mark Brainliest And 50 Points Brainly Com



X Sqrt 2y 1 Y 2 X 0 Y 0 About The Line Y 3 Youtube
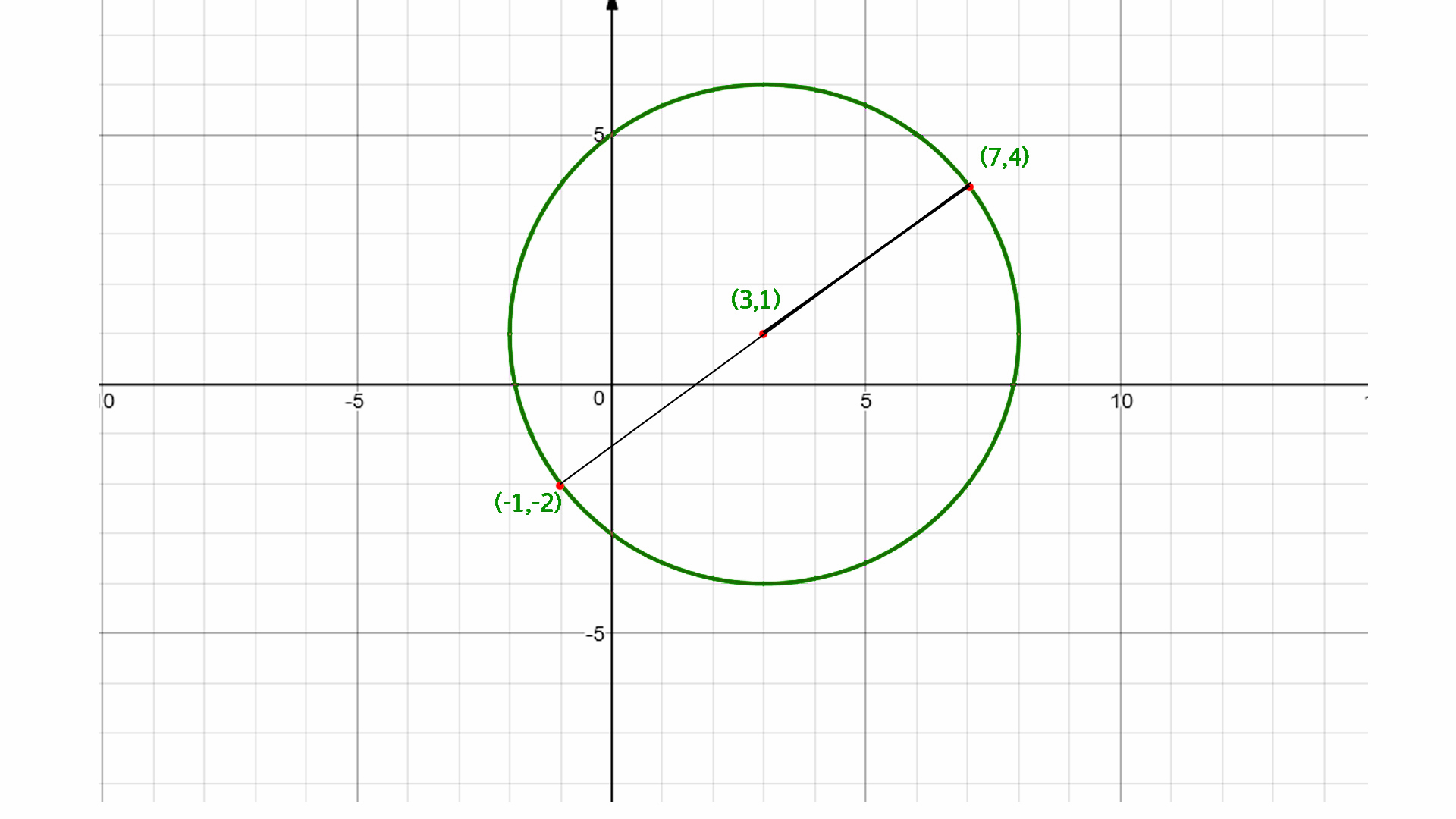


Find The Center Of The Circle Using Endpoints Of Diameter Geeksforgeeks
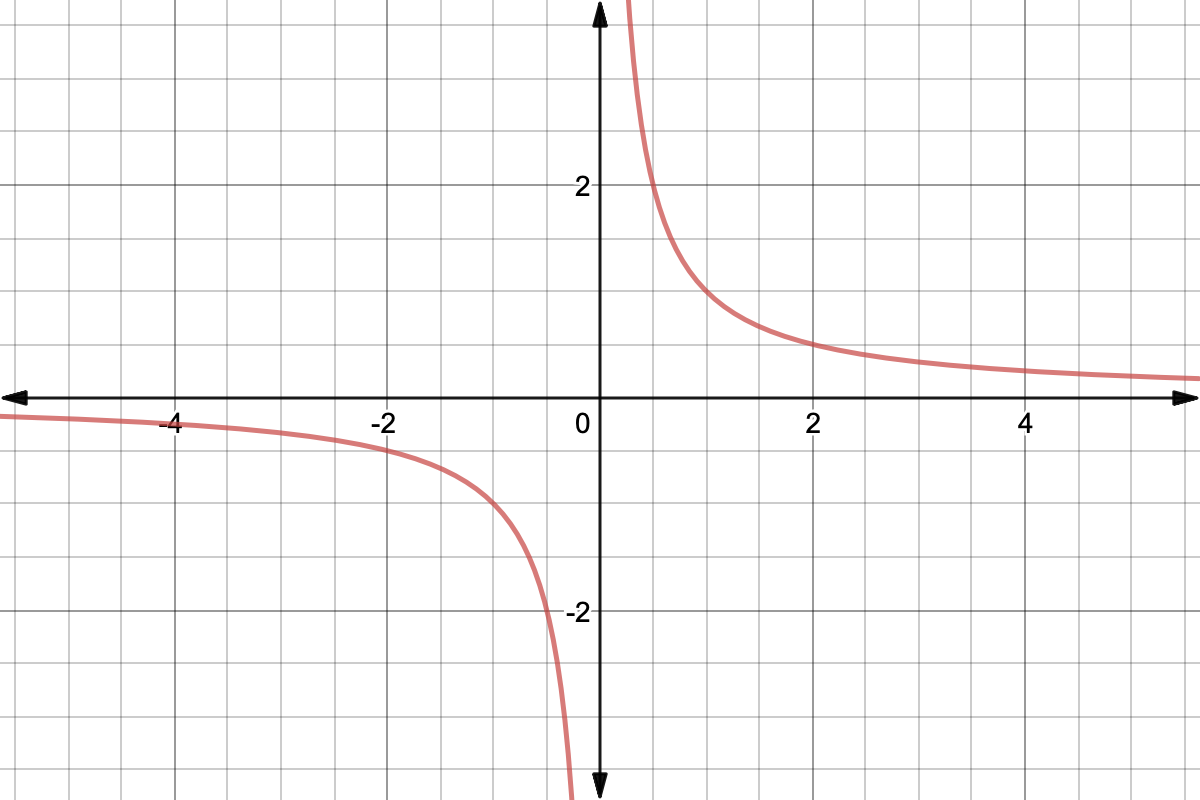


Inversely Proportional Functions In Depth Expii
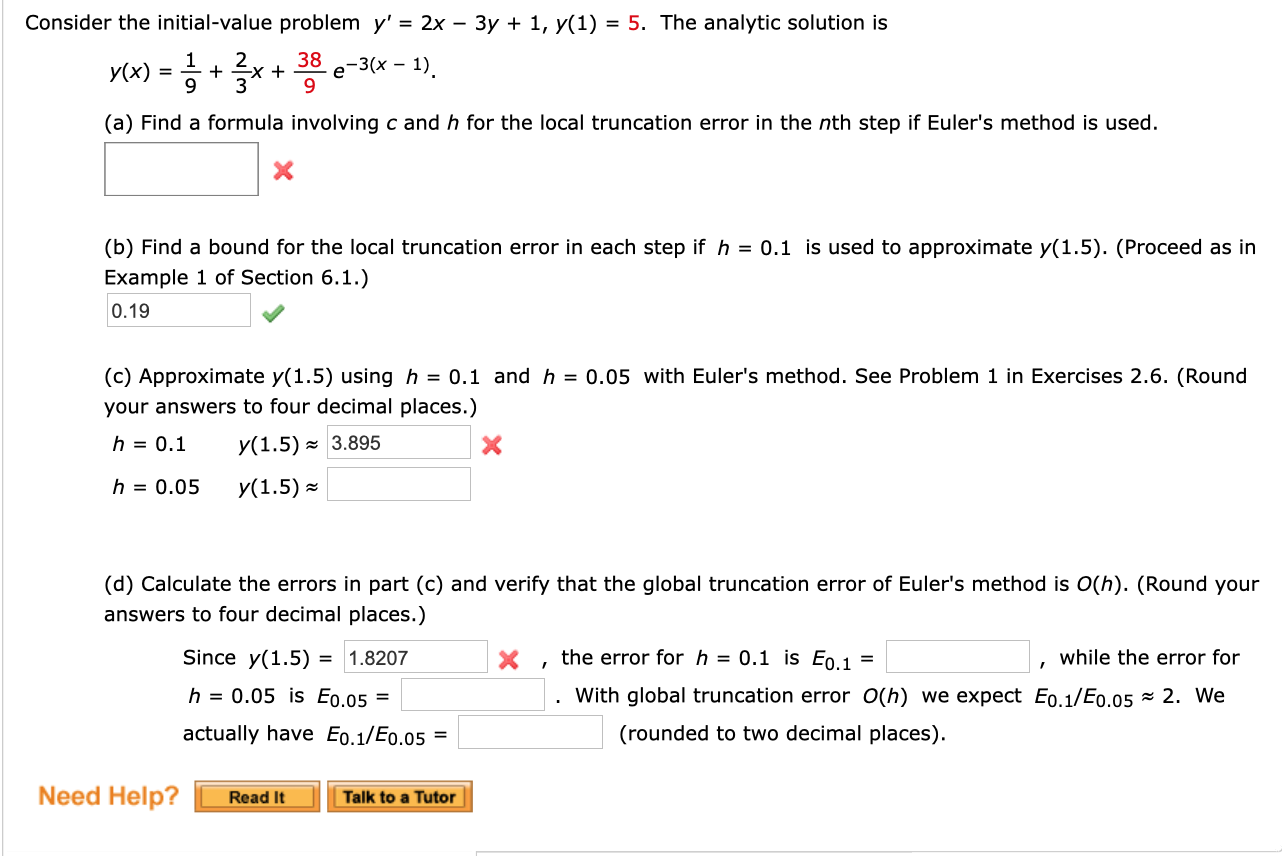


Solved Consider The Initial Value Problem Y 2x 3y Chegg Com
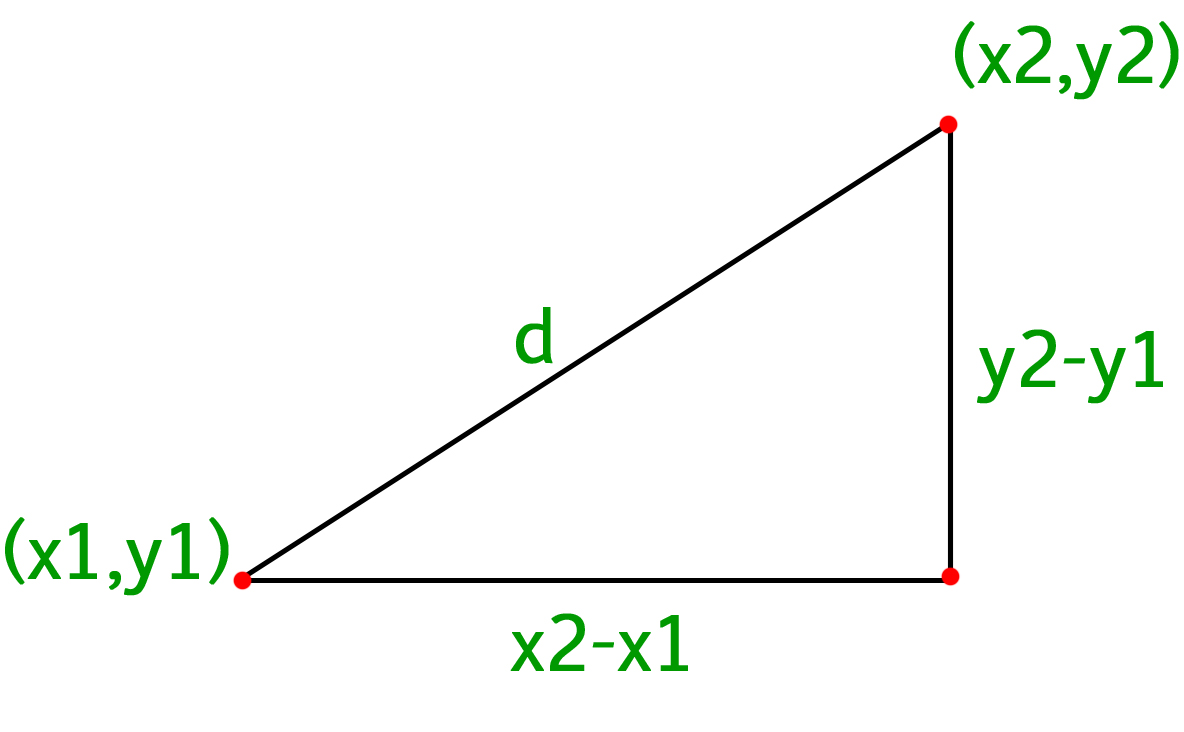


Program To Calculate Distance Between Two Points Geeksforgeeks



Ppt Algebra1 The Slope Formula Powerpoint Presentation Free Download Id


Using The Slope Formula Wmv Youtube


Answered 1 X2 R 2 X 2 0 About The Y Axis Bartleby



Solve The Following System Of Equation By Matrix Method 1 X Y Z 6 X Y Z 4 X 2y 2z 1 2 X Y 3z 10 X Y Z 2 2x 3y 4z 4 3 X Y Z 6 X 2y 3z 6 X Y Z 2 4 2x Y Mathematics Topperlearning Com Yv1op566



Slope And Y Intercept From Equation Video Khan Academy



Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy



Bernoulli Differential Equation X Dy Dx Y 1 Y 2 Differential Equations Math Videos How To Become



Slope Formula Y2 Y1 X2 X1 Youtube


